Building and Manipulating Atoms

Overview

Teaching: 25 min
Exercises: 25 min

Questions

• How can I build molecules and bulk structures more efficiently?

• How can I create supercells and point defects?

Objectives

• Build a molecule using the built-in database

• Build a crystal using built-in crystal structure types

• Build (optimal) supercell expansions

• Remove, add or swap atom(s) to create point defects

Code connection

In this episode we explore the ase.build module, which contains tools for building structures using parameters rather than detailed lists of positions.

A set of simple molecules are pre-defined in ASE

• Definitions for a set of simple molecules (the “G2” set and the “S22” set) are included with ASE.
• So in fact the easiest way to get an N2 molecule is with ase.build.molecule.

import ase.build
from ase.visualize import view

g2_n2 = ase.build.molecule('N2')
view(g2_n2, viewer='ngl')

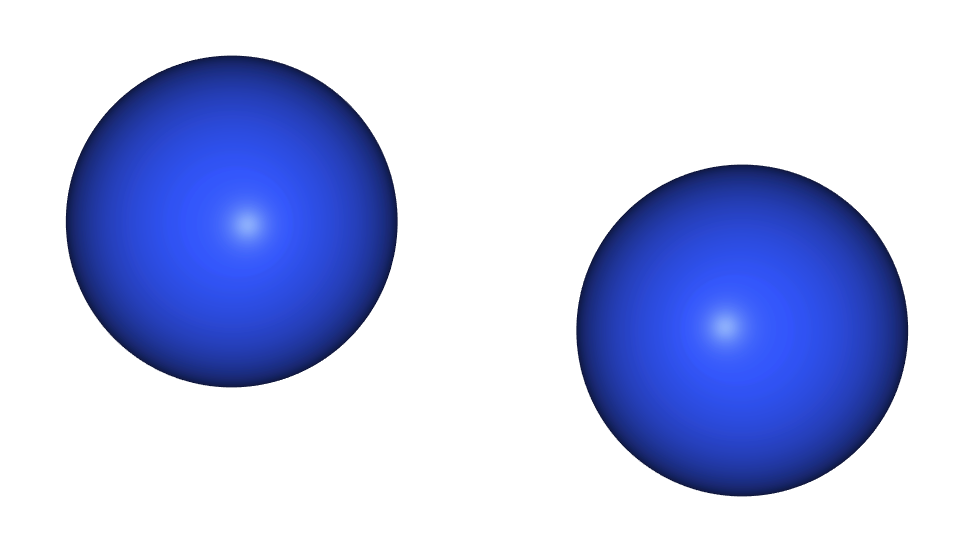
• If we inspect the type of g2_n2 we see that it is an Atoms object, just like that we created manually in earlier episodes.

type(g2_n2)

ase.atoms.Atoms

• And it’s just as easy to get more interesting things like a buckyball!

view(ase.build.molecule('C60'), viewer='ngl')

There are pre-defined lattice parameters and crystal types to create bulk systems

• The equivalent tool to build crystals is ase.build.bulk.
• This includes lattice parameters for some elemental reference states; the list is in the code here.
• So we get copper, for example, with very little work:

view(ase.build.bulk('Cu', cubic=True), viewer='ngl')

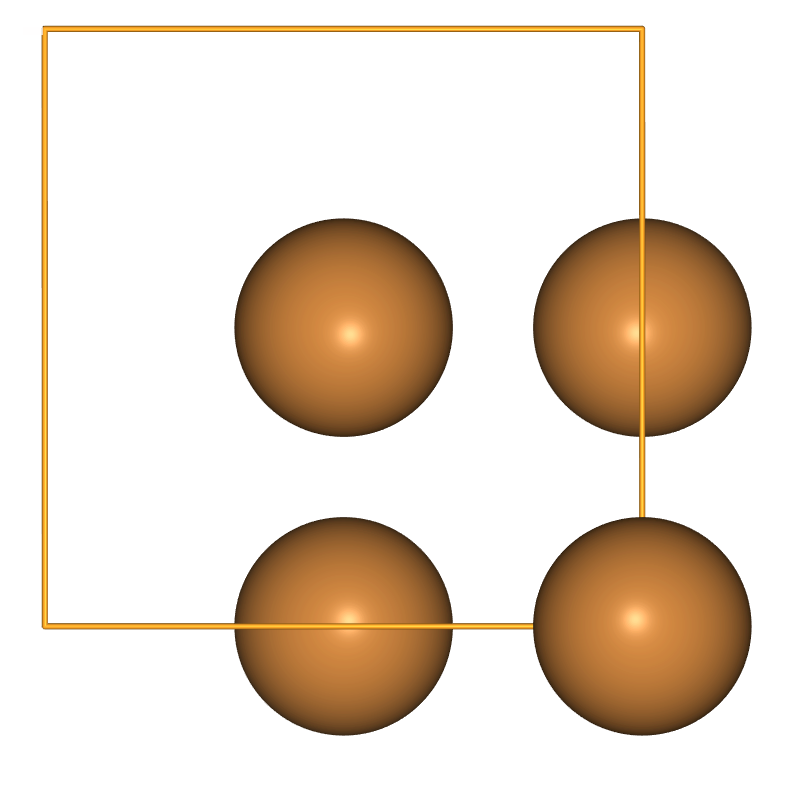
• To create ZnS in the zincblende structure we have to provide the crystalstructure and the lattice parameter a.

view(
    ase.build.bulk('ZnS',
                   crystalstructure='zincblende',
                   a=5.387,
                   cubic=True), 
    viewer='ngl'
)

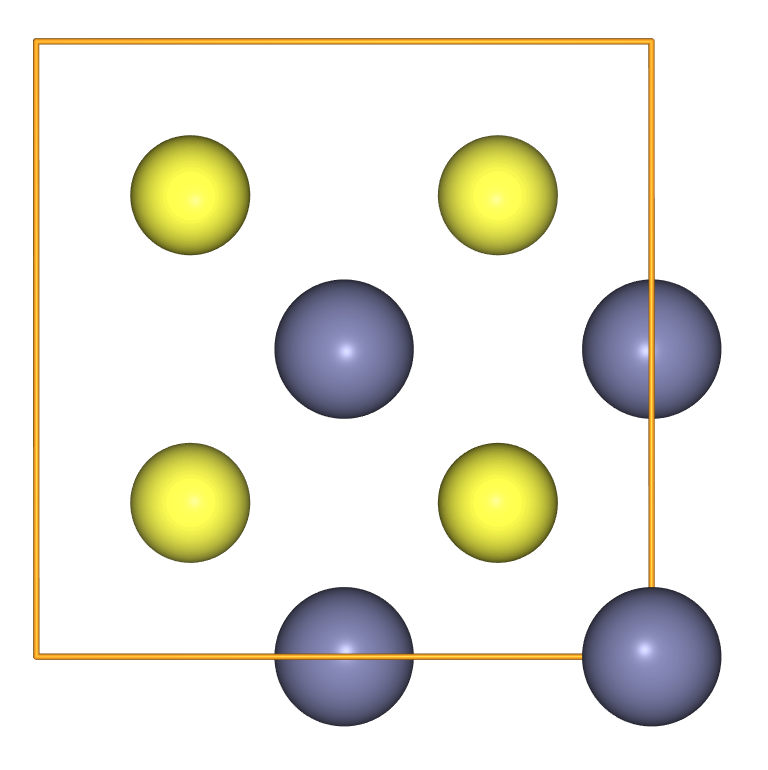
A compact notation can be used to create a supercell

• Supercell expansions of a unit cell are commonly used when modelling, for example, lattice dynamics or defect systems.
• A compact notation can be used to create the repeated unit cell.
• Start by creating a cubic unit cell of Si.

si = ase.build.bulk('Si', cubic=True)
view(si, viewer='ngl')

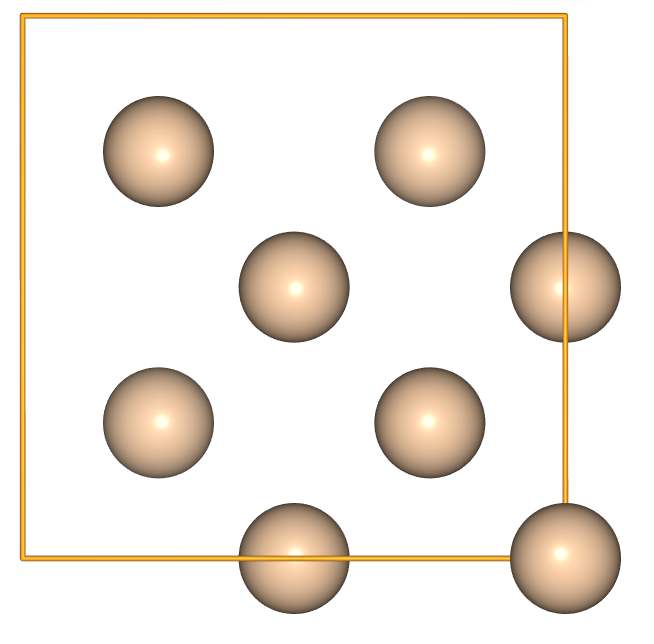
• Use integer multiplication to perform equal repetition in each direction:

view(si * 4, viewer='ngl')

• Use a 3-list or 3-tuple to perform unequal repetitions in each direction:

view(si * [2, 4, 1], viewer='ngl')

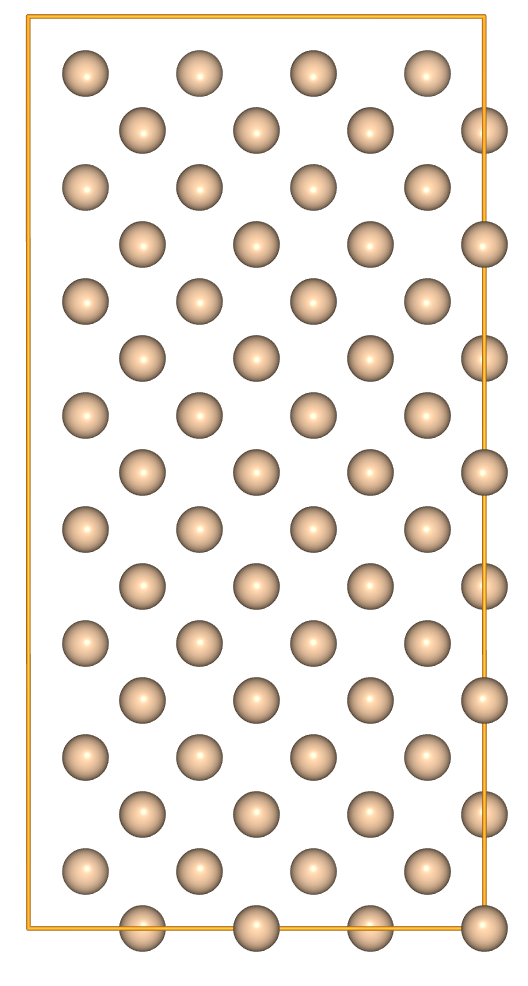
Cell parameters can be inspected using the Atoms.cell attribute

• When we model dilute defects it can be useful to use cubic supercell expansions, as these will maximise the minimum distance between periodic images.
• Our starting point for this is often a non-cubic primitive cell.

si_prime = ase.build.bulk('Si')
view(si_prime, viewer='ngl')

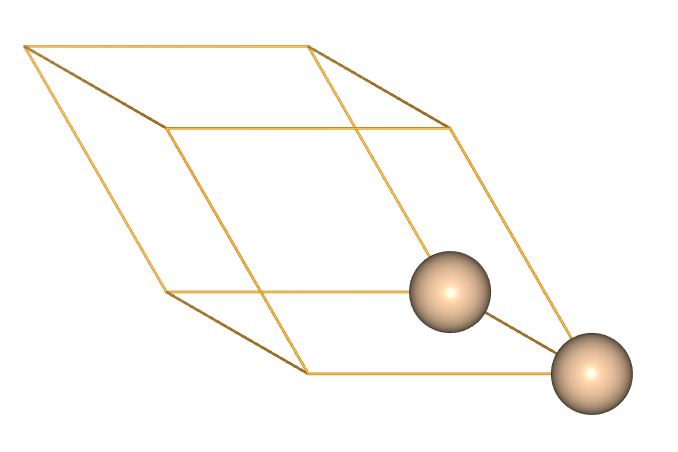
• We can inspect the cell parameters using the Atoms.cell attribute.

si_prime.cell

Cell([[0.0, 2.715, 2.715], [2.715, 0.0, 2.715], [2.715, 2.715, 0.0]])

• We find that Atoms.cell returns an instance of the ASE Cell class.
• The Cell object represents three lattice vectors forming a parallel epiped.

ASE can search for the matrix which gives the most cubic supercell

• Once we have a primitive cell, we can perform a numerical search to find the optimal 3x3 array for forming the most cubic supercell; this process may take a few seconds.
• We specify three positional arguments: unit cell parameters, the target size of the supercell, and the target shape. For more information, you can inspect the docstring.

Academic background

This algorithm is described in more detail in the ASE docs, and was developed to support supercell doping calculations

optimal_array = ase.build.find_optimal_cell_shape(si_prime.cell, 4, 'sc', verbose=True)

target metric (h_target):
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
normalization factor (Q): 0.184162
idealized transformation matrix:
[[-1.  1.  1.]
 [ 1. -1.  1.]
 [ 1.  1. -1.]]
closest integer transformation matrix (P_0):
[[-1  1  1]
 [ 1 -1  1]
 [ 1  1 -1]]
smallest score (|Q P h_p - h_target|_2): 0.000000
optimal transformation matrix (P_opt):
[[-1  1  1]
 [ 1 -1  1]
 [ 1  1 -1]]
supercell metric:
[[5.43 0.   0.  ]
 [0.   5.43 0.  ]
 [0.   0.   5.43]]
determinant of optimal transformation matrix: 4

• We can then pass the 3x3 array to ase.build.make_supercell to form a cubic supercell.

cubic_Si_expansion = ase.build.make_supercell(si_prime, optimal_array)
view(cubic_Si_expansion, viewer='ngl')

cubic_Si_expansion.cell

Cell([5.43, 5.43, 5.43])

• We find that, as expected, this is equal to the Si cubic crystal structure pre-defined in ASE.

si = ase.build.bulk('Si', cubic=True)
si.cell

Cell([5.43, 5.43, 5.43])

An Atoms object can be treated as an array of Atom objects

• An Atoms object can be treated as a list of Atom objects which we can iterate over.
• Atom is a class for representing….you guessed it…a single atom.

crystal = ase.build.bulk('ZnS',
                   crystalstructure='zincblende',
                   a=5.387,
                   cubic=True)

for atom in crystal:
    print(atom.symbol, atom.position, atom.mass)

Zn [0. 0. 0.] 65.38
S [1.34675 1.34675 1.34675] 32.06
Zn [0.     2.6935 2.6935] 65.38
S [1.34675 4.04025 4.04025] 32.06
Zn [2.6935 0.     2.6935] 65.38
S [4.04025 1.34675 4.04025] 32.06
Zn [2.6935 2.6935 0.    ] 65.38
S [4.04025 4.04025 1.34675] 32.06

• Numpy-like array indexing and slicing is also available.
• For example, we can combine indexing with list comprehension to return the zinc sub-lattice.

zinc_indices = [i for i, atom in enumerate(crystal) if atom.symbol == 'Zn']
zinc_sublattice = crystal[zinc_indices]
view(zinc_sublattice, viewer='ngl')

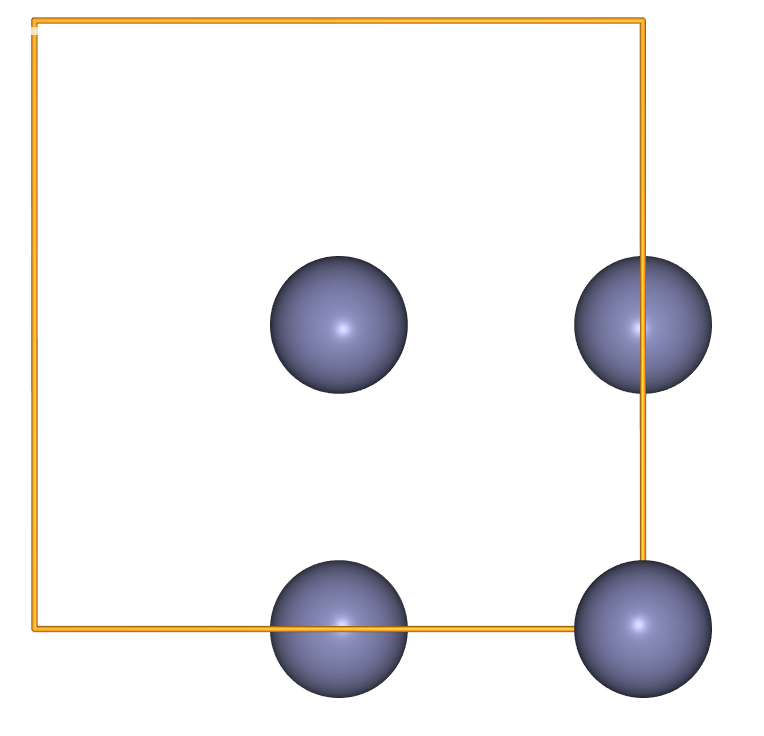
• When we index multiple atoms, an Atoms object is returned.

type(zinc_sublattice)

ase.atoms.Atoms

Methods and operations can be used to create point defects

• An individual Atom can be appended to create an interstitial defect.

from ase import Atom
composite = zinc_sublattice.copy()
composite.append(Atom('He', position=(1.34675, 4.04025, 4.04025)))
view(composite, viewer='ngl')

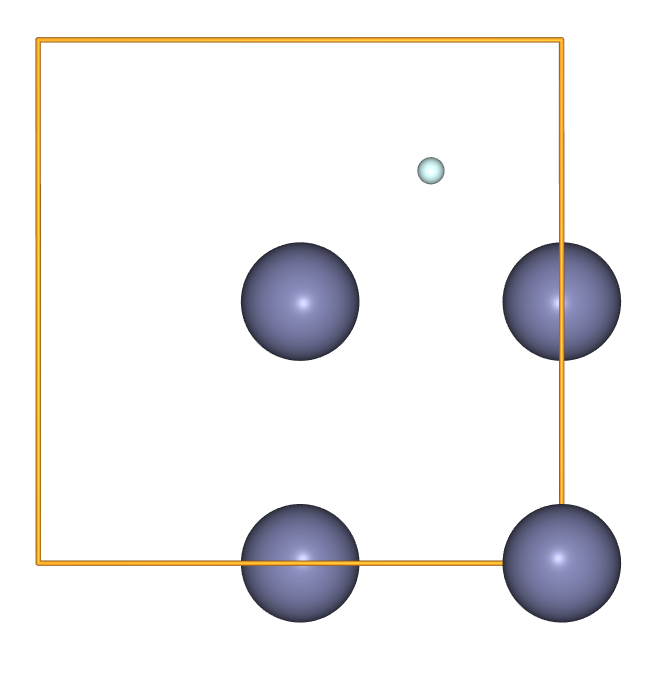
• While Atoms is not exactly a regular Python data collection, it plays nicely with the delete operation.
• We can use this operation to create, for example, a zinc-vacancy defect:

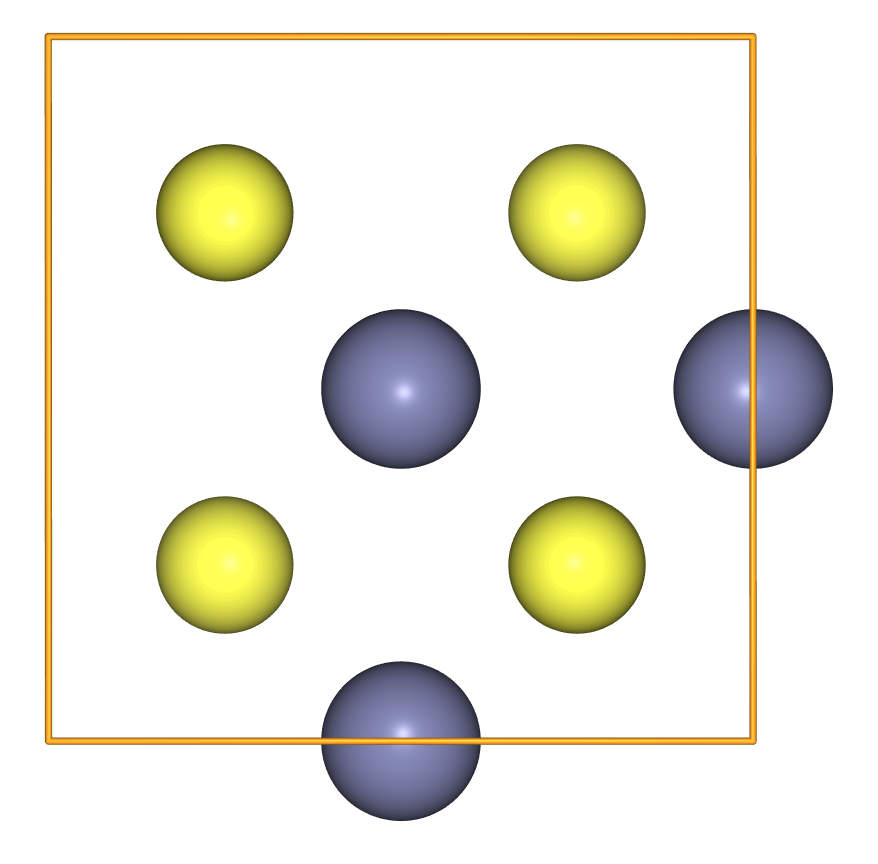
zinc_vacancy = crystal.copy()
del zinc_vacancy[0]
view(zinc_vacancy, viewer='ngl')

• To create antisite disorder, we can swap two positions from the positions array.

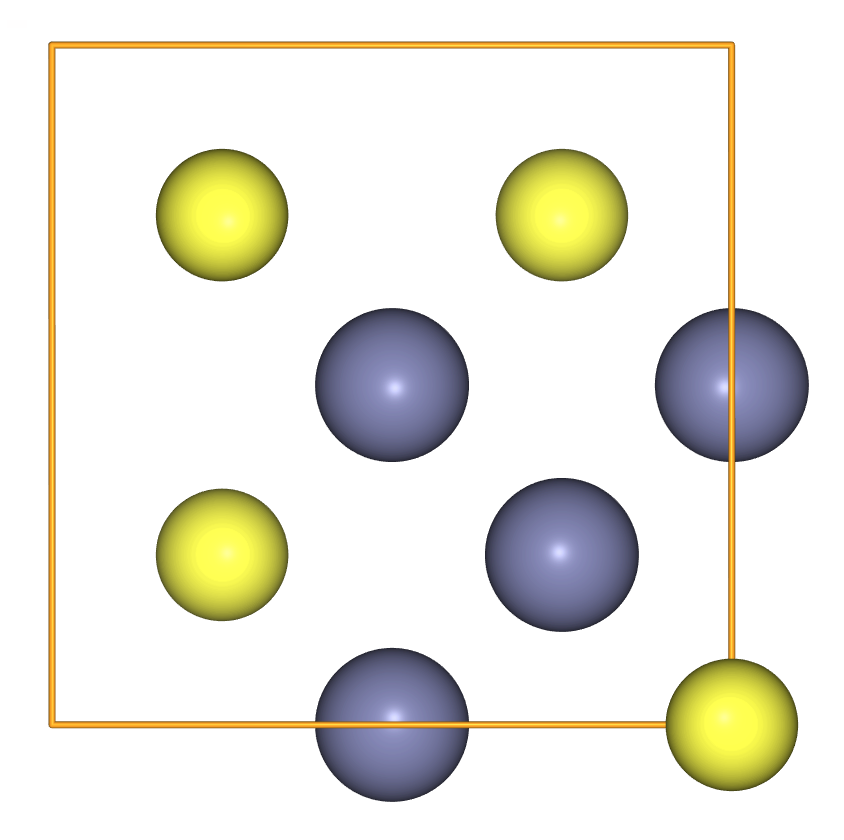
antisite = crystal.copy()
antisite.positions[[0, 1]] = antisite.positions[[1, 0]]
view(antisite, viewer='ngl')

Exercise: Distorted sphalerite

It is possible to combine entire Atoms with +. In this case, the first Atoms takes precedence to determine the cell parameters. Use this to create a distorted sphalerite cell, with the S sublattice translated along the x-coordinate relative to the Zn sublattice

Solution

sulfur_indices = [i for i, atom in enumerate(crystal) if atom.symbol == 'S']
sulfur_sublattice = crystal[sulfur_indices]
sulfur_sublattice.translate([.3, 0., 0.])
view(zinc_sublattice + sulfur_sublattice, viewer='ngl')

Exercise: Water animation

Create an animation of a water molecule being wrapped in a C60 cage (or something even cooler!)

Hints:

• The GIF animation will need to be generated with a list of Atoms objects
• Molecules can be combined with +
• To get the wrapping effect we need to keep adding atoms that are near to the atoms already added
• To avoid writing too much repetitive code, use Python’s looping tools

Solution

water = ase.build.molecule('H2O')
water.center()

bucky = ase.build.molecule('C60')
bucky.center()

start_atom = 36
distances = bucky.get_all_distances()[start_atom]
sorted_bucky_indices = sorted(enumerate(distances),
                              key = (lambda x: x[1]))
sorted_bucky_indices = [i for i, _ in sorted_bucky_indices]
sorted_bucky = bucky[sorted_bucky_indices]

frames = [water.copy()]

for i in range(len(sorted_bucky)):
    frames.append(water + sorted_bucky[:i + 1])

from ase.io.animation import write_gif
_ = write_gif('wrapped_molecule.gif', frames)

Key Points

• A set of simple molecules are pre-defined in ASE

• There are pre-defined lattice parameters and crystal types to create bulk systems

• A compact notation can be used to create a supercell

• Cell parameters can be inspected using the Atoms.cell attribute

• ASE can search for the matrix which gives the most cubic supercell

• An Atoms object can be treated as an array of Atom objects

• Methods and operations can be used to create point defects